题意
定义在排列上进行操作为删去所有存在一个相邻的数大于自身的数，若只剩下一个数则中止。
给定 ，计数所有长度为 的可以进行恰好 次操作后中止的排列。
思路
对于本题，思考时切入点较多，不过经过交流后我认为最后得到的做法应该都是本质相同的，本文提供笛卡尔树为基本视图的路径。
对于排列的大小关系一类的问题，不难想到转化为笛卡尔树。此时，操作的形式变为删去所有一度点与（除了最左与最右）二度点，将原先的二度点替换为一条边，即树收缩（tree contraction）操作：
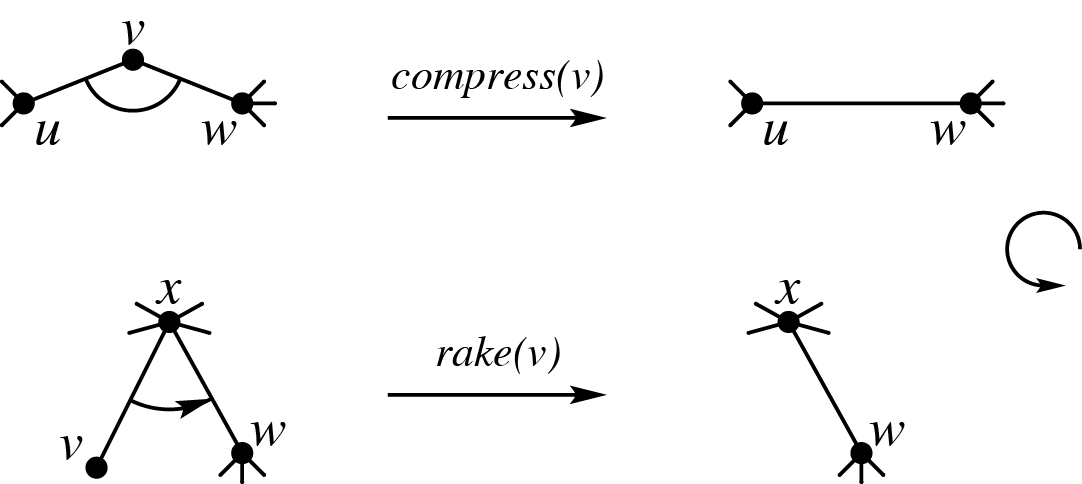rake and compress
如果你听说过 top cluster 理论，你会知道这个过程只会执行 次，不过这个理论与本文并无关系，而且我们有一个更为简单的证明：因为一个不被删去的点两边都是被删去的点，故而每次操作都将删去一半的点。
在开始刻画状态之前，我们需要进一步的简化操作轮数的计算（我们称将某个子树删空需要的操作次数为操作轮数，注意并不一定是其根节点删除的时间），我们发现对于非根结点 ，其操作轮数是其两个子树的操作轮数的 （当其一个子树为空时，下回合它就会被删除），特殊的，我们认为 最左/最右 的结点的 左子树/右子树 的操作轮数为无穷大（之后称 最左/最右 结点为端点）
对于笛卡尔树上的 DP，常见的形式是自底向上进行多区间合并，不过本题我们需要记录区间自身的信息，故这种方式并不可行。由于本题中区间之间的影响较小，考虑自顶向下拆分区间，我们设 表示包含 个结点的、删除时间为 的笛卡尔树数量，不过注意到端点处转移会略有不同，所以还需要记录端点的状态。
一个朴素的想法是记录 表示其左右端点的存在情况，不过显然，当最大值插入之后（由于其不能被删除所以需要特殊讨论），所有位置都有了一个端点，并且只有左端点和只有右端点是等价的，于是可以简化为 表示其存在 一个/两个 端点。
转移较为自然，分为两部分：
将长度为 的序列枚举分割为 ，首先我们需要把 个数分配到左右两个区间，这个系数显然为 。
一个端点的状态可以令有端点的一侧操作轮数为 ，另一侧小于等于 轮；或无端点的一侧操作轮数为 ，另一侧小于等于 轮（这两种当全取等于的时候实际上是同一种，以下不讨论这类问题，由读者自行决定如何去重）。
两个端点的状态则可以令两侧全为 ，或者任意一侧为 ，另一侧小于等于 。
该点为最左或最右，此时转移系数为 。
一个端点的状态可以建立另一个端点，此时令间的操作轮数为 ，或者延续之前的端点，此时中间的操作轮数为 。
两个端点的状态可以选择随意放置在左侧或右侧（转移系数为 ）， 不变。
实际的转移顺序为按照长度顺序，当然你可以写记搜。
对于根节点，其操作轮数是两个子树的 ，容易处理。
注意到转移过程中存在一个偏序的贡献，可使用前缀和优化至 。
状态数 ，转移 ，总时间复杂度为 。
观察第一维贡献形式看起来可以卷积啊，不过以我的多项式水平这种东西就留给后人了。
CODE
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
| #include<cstdio>
#include<algorithm>
using namespace std;
using ll=long long;
const int N=1010,FSIZE=1<<26;
int tn,n,m,mo,f[N][20][4],s[N][20][4],C[N][N];
char BuF[FSIZE],*InF=BuF;
template<typename T>void read(T &x){
for(;48>*InF||*InF>57;++InF);
for(x=0;47<*InF&&*InF<58;x=x*10+(*InF++^48));
}
int add(int x,int y){if((x+=y)>=mo) x-=mo;return(x);}
void add(int &x,ll y){x=(x+y)%mo;}
int main(){
fread(BuF,1,FSIZE,stdin);
read(n);read(m);read(mo);
if(m>__lg(n)+1){
printf("0\n");
return(0);
}
f[0][1][0]=f[0][1][1]=f[1][1][0]=f[1][1][1]=1;
for(int i=1;i<=m;++i)
s[0][i][0]=s[1][i][0]=s[0][i][1]=s[1][i][1]=1;
for(int i=C[0][0]=1;i<=n;++i)
for(int j=C[i][0]=1;j<=i;++j)
C[i][j]=add(C[i-1][j-1],C[i-1][j]);
for(int i=2;i<n;++i)
for(int j=0;j<=m;++j){
for(int k=2;k<i;++k){
ll x=C[i-1][k-1];
add(f[i][j][0],
(ll)f[k-1][j-1][1]*s[i-k][j-1][0]%mo*x+
(ll)s[k-1][j-1][1]*f[i-k][j][0]%mo*x);
add(f[i][j][1],
(ll)f[k-1][j-1][1]*f[i-k][j-1][1]%mo*x+
(ll)f[k-1][j][1]*s[i-k][j-1][1]%mo*x+
(ll)s[k-1][j-1][1]*f[i-k][j][1]%mo*x);
}
add(f[i][j][0],ll(f[i-1][j-1][1]+f[i-1][j][0]));
add(f[i][j][1],(ll)f[i-1][j][1]*2);
s[i][j][0]=add(s[i][j-1][0],f[i][j][0]);
s[i][j][1]=add(s[i][j-1][1],f[i][j][1]);
}
int ans=f[n-1][m][0]+f[n-1][m][0];
for(int i=2;i<n;++i){
int x=C[n-1][i-1];
add(ans,(ll)f[i-1][m][0]*s[n-i][m-1][0]%mo*x);
add(ans,(ll)s[i-1][m-1][0]*f[n-i][m][0]%mo*x);
add(ans,(ll)f[i-1][m][0]*f[n-i][m][0]%mo*x);
}
printf("%d\n",ans);
return(0);
}
|